Application of optimal control techniques to natural systems management
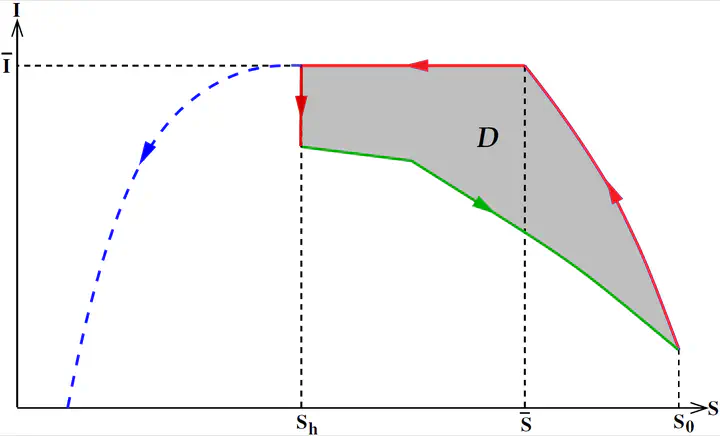
Optimal control techniques have numerous applications in engineering and real world problems. This thesis is devoted to using these techniques in two contexts, mining and epidemiology, dividing this document in two respective parts. In the first part related to mining, we work with the continuous formulation of the Open Pit Problem consisting of finding the optimal shape of an opencast mine representing its profile by a continuous function. Optimality in this context corresponds to maximizing the profit of mineral extraction. We introduce for the first time optimal control models of this problem. We present optimality conditions of solutions along with numerical experiments using local and global methods. Another relevant problem in this context corresponds to the Sequential version of the Open Pit Problem, which consists of scheduling an extraction program over consecutive time frames (for example, a profile each 6 months), finding nested profiles maximizing a discounted profit. We proposed a novel semi-continuous model to obtain solutions of the sequential problem and we use it to present for the first time, to the best of our knowledge, numerical solutions of a three dimensional case (a possible real world mine) including the original Open Pit Problem (case with a single time-frame). In the second part we deal with optimal control problems minimizing the maximum value of a state. This problematic was inspired by Covid-19, where hospitals and ICU beds were overcrowded due to a high amount of simultaneous infections. We present four different reformulations of this kind of optimal control problem as a Mayer one, each one having its pros and cons. We present the numerical performance of each formulation in an academic example and in a more realistic SIR model where the problem corresponds to minimizing the peak of infectious compartment with integral constraint in the control. With respect to the latter problem, we prove analytically that the structure of the optimal control is null-singular-null and we used it to assess numerical solutions.